Chaînes de Markov

Une chaîne markovienne (du nom du mathématicien russe Andrei Andreiëvich Markov) est constituée d'une succession (ou séquence) d'évènements, généralement indiqués comme états, caractérisée par deux propriétés:

- l'ensemble des évènements et de leurs issues possibles est fini;
- l'issue de chaque évènement dépend seulement (ou au maximum) de l'évènement immédiatement précédent.

Avec la conséquence qu' une valeur de probabilité correspond à chaque transition d'un évènement à l'autre.

Dans le domaine scientifique, le modèle des chaînes markoviennes est utilisé pour analyser les successions d'évènements économiques, biologiques, physiques, etc. Dans le domaine des études linguistiques ses applications ont pour objet les combinaisons possibles des diverses unités d'analyses sur l'axe des relations syntagmatiques (l'une après l'autre).

Dans T-LAB l'analyse des chaînes markoviennes concerne deux types de séquences:

" celles concernant les relations entre unités lexicales (mots, lemmes ou catégories) présentes dans le corpus en analyse;
" celles présentes dans des fichiers externes préétablis par l'utilisateur.

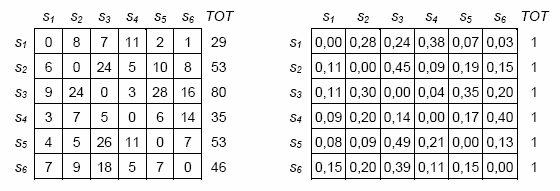
Dans les deux cas, en premier lieu sont constitués des tableaux carrés dans lesquels sont reportées les occurrences des transitions, c'est-à-dire des quantités qui indiquent le nombre de fois qu'une unité d' analyses précède (ou suit) l'autre. Successivement, les occurrences des transitions sont transformées en valeurs de probabilité (voir image suivante).

Pour plus d'informations voir Analyse des Séquences.