Multidimensional Scaling (MDS)

MDS is a set of data analysis techniques that allow us to analyse similarity matrices in order to provide a visual representation of the relationships among the data within a space of reduced dimensions.

T-LAB uses a type of MDS (Sammon's method) in order to represent the relationships among the lexical units or among the thematic nuclei (see Co-Word Analysis and Modeling of Emerging Themes).

The input tables are constituted by square matrices which contain proximity values (dissimilarities) derived from the calculation of an association index.

The results obtained, like those of the correspondence analysis, allow us to interpret both the relationships between the "objects" and the dimensions that organize the space in which they are represented.

The degree of correspondence between the distances among points implied by the MDS map and the matrix input is measured (inversely) by a Stress function. The lesser the stress value (e.g. < 0.10), the greater the goodness of the obtained adjustment.

The stress formula (Sammon's method) is the following:

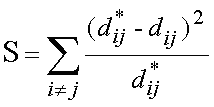
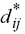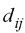Where stands for the distance between two points (ij) within the input matrix and stands for the distance between the same points (ij) within Sammon's map.