Markov chains

A Markov chain (from the name of the Russian mathematician Andrei Andreiëvich Markov) consists in a succession (or sequence) of events, generally suitable as status, characterized by two properties:

- the series of the events and their possible outcomes is a finite set;
- the outcome of each event depends only (or at the most) on the immediately precedent event.

With the consequence that a probability value corresponds to every transition from one event to the other.
In scientific domain, the Markovian chains model is used to analyse the succession of economic, biological, physical events etc. In the domain of linguistic studies its application concerns the possible combinations of the various analysis units on the syntagmatic axis (one item after the other).

In T-LAB the analysis of the Markovian chains relates to two types of sequences:

· those concerning the relationships between lexical units (words, lemmas or categories) present in the corpus under analysis;
· those present in external files prepared by the user.

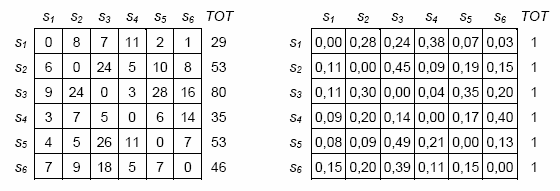
In both cases, to start with, some square tables are constructed in which the occurrence of transitions is recorded, that is the quantity that indicates the number of times in which an analysis unit precedes (or follows) the other. Subsequently, the transition occurrences are transformed into probability values (see the following images):

For further information see Sequence Analysis