|
www.tlab.it
Chi-Square
Chi-square is a statistical test to check if the
frequency values obtained by a survey and recorded in some
cross-table, are significantly different from the theoretical ones
(the "expected" values).
Generally, T-LAB applies this test to (2 x
2) tables and the threshold value is 3.84 (df = 1; p.
0.05) or 6.64 (df = 1; p. 0.01).
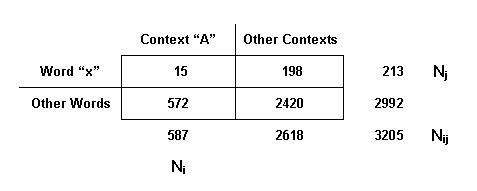
For example, in order to verify the significance of a
word ("x") occurrences within a context unit ("A") the test is
applied to a table as follows:
The chi-square formula, in its
simplified version, is the following:
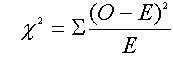
where
"O" and "E" stand respectively for the observed frequencies and the
expected ones.
For each cell, the expected (E) occurrences are
calculated as follows: (Ni x Nj)/Nij.
Following the above example the CHI value is equal to
19.38.
Since it is greater than the critical value, the null
hypothesis (absence of meaningful difference) can be
rejected.
|