Catena Markoviana

Una catena markoviana (dal nome del matematico russo Andrei Andreiëvich Markov) è costituita da una successione (o sequenza) di eventi, generalmente indicati come stati, caratterizzata da due proprietà:

- l'insieme degli eventi e dei loro possibili esiti è finito;
- l'esito di ogni evento dipende solo (o al massimo) dall'evento immediatamente precedente.

Con la conseguenza che ad ogni transizione da un evento all'altro corrisponde un valore di probabilità.

In ambito scientifico, il modello delle catene markoviane è utilizzato per analizzare le successioni di eventi economici, biologici, fisici, ecc. Nell'ambito degli studi linguistici le sue applicazioni hanno come oggetto le possibili combinazioni delle varie unità di analisi sull'asse delle relazioni sintagmatiche (una dopo l'altra).

In T-LAB l'analisi delle catene markoviane concerne due tipi di sequenze:

- quelle concernenti le relazioni tra unità lessicali (parole, lemmi o categorie) presenti nel corpus in analisi;
- quelle presenti in file esterni predisposti dall'utilizzatore.

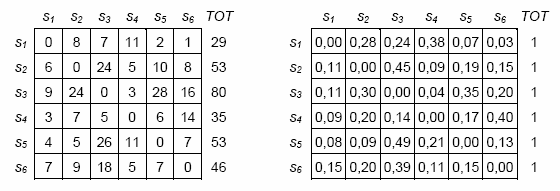
In entrambe i casi, in primo luogo vengono costruite tabelle quadrate in cui sono riportate le occorrenze delle transizioni, cioè quantità che indicano il numero di volte in cui una unità di analisi precede (o segue) l'altra. Successivamente, le occorrenze delle transizioni vengono trasformate in valori di probabilità (vedi immagini seguenti).

Per ulteriori informazioni vedi Analisi delle Sequenze.